Mastering Self-Attention: Queries, Keys, and Values in Action

Self-attention, or scaled dot-product attention, computes a representation of each word in a sequence by considering all other words in the sequence. This allows the model to capture contextual relationships between words. In the attached figure, each word (e.g., "Time," "for," "a," "break") attends to every other word through a combination of operations.

Key Components in Self-Attention

The self-attention mechanism relies on three key components:

1. Queries (Q): Query vectors represent the token for which the attention is being calculated. They act as a search mechanism, helping the model determine how much focus should be given to each other token in the sequence with respect to the current token.
2. Keys (K): Key vectors represent each token in the sequence and serve as points of reference for determining relevance. When calculating attention, each query vector is compared with all key vectors in the sequence to assess the similarity or alignment with each token.
3. Values (V): Value vectors contain the actual information about each token that may be passed along to the next layers. Once the attention weights are calculated using the query-key pairs, they are applied to the value vectors to get the final output representation of each token.

For each word in the sequence, we compute a weighted sum of the values where the weights are determined by the similarity between the query and the keys.

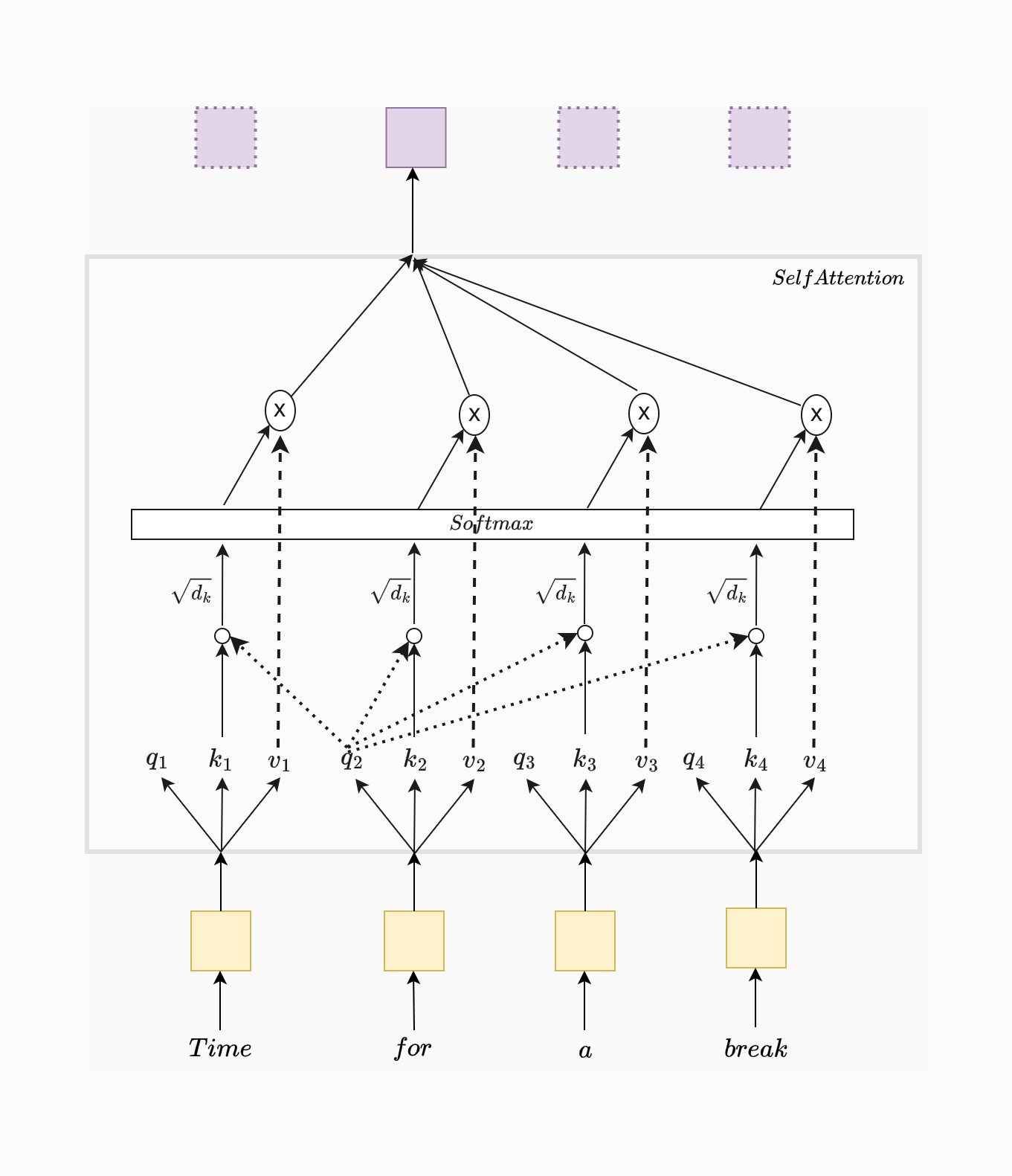
How self attention works

Step 1: Creating Q, K, and V Vectors

As shown in the figure, each word is associated with a query, key, and value vector (labeled as $q_i$, $k_i$, and $v_i$ for each word $i$). These vectors are learned during training.

Given an input sequence with nnn words, we create matrices Q, K, and V:

Step 2: Computing Attention Scores

To determine how much attention each word should pay to the others, we compute the dot product of the query with each key:

This gives a similarity measure between word $i$ and word $j$.

To prevent large values, we scale these scores by $\sqrt{d_k}$, where $d_k$ is the dimension of the key vectors:

Step 3: Applying Softmax

Next, we apply the softmax function to the scaled scores to convert them into probabilities. This helps determine the relative importance of each word in the sequence:

These weights, shown in the figure under the "Softmax" layer, indicate how much attention each word (column) should pay to other words (rows).

Step 4: Weighted Sum of Values

Finally, we compute the output for each word by taking a weighted sum of the value vectors:

This weighted sum, shown at the top of the figure, represents each word as a combination of all the other words, weighted by their importance.

class SingleHeadSelfAttention(torch.nn.Module):
    def __init__(self, embed_size):
        super(SingleHeadSelfAttention, self).__init__()
        self.embed_size = embed_size

        # Linear layers for Q, K, and V transformations
        self.values = torch.nn.Linear(embed_size, embed_size, bias=False)
        self.keys = torch.nn.Linear(embed_size, embed_size, bias=False)
        self.queries = torch.nn.Linear(embed_size, embed_size, bias=False)

    def forward(self, values, keys, query, mask=None):
        # Input shapes (sequence_length, embed_size)
        seq_len = values.shape[1]

        # Apply linear transformations to get Q, K, V matrices
        values = self.values(values)   # (sequence_length, embed_size)
        keys = self.keys(keys)         # (sequence_length, embed_size)
        queries = self.queries(query)  # (sequence_length, embed_size)

        # Calculate dot-product attention scores
        energy = torch.matmul(queries, keys.transpose(-2, -1))  # (sequence_length, sequence_length)

        # Scale the attention scores by √d_k
        scaling_factor = self.embed_size ** 0.5
        energy /= scaling_factor

        # Apply softmax to get normalized attention weights
        attention = F.softmax(energy, dim=-1)  # (sequence_length, sequence_length)

        # Compute the weighted sum of values
        out = torch.matmul(attention, values)  # (sequence_length, embed_size)

        return out

Multi Head Attention

Multi-head attention allows the model to capture diverse types of relationships and dependencies in the data by computing multiple attention distributions, each focusing on a different subspace of the embedding.

In a single-head attention mechanism, each token's representation is influenced by all other tokens based on a single attention distribution. However, this single perspective may not fully capture the complex and varied relationships present in language. Multi-head attention addresses this limitation by performing multiple attention calculations in parallel, each with a different set of projections for queries, keys, and values. These independent attention heads allow the model to learn various aspects of the relationships between tokens, providing a richer contextual understanding.

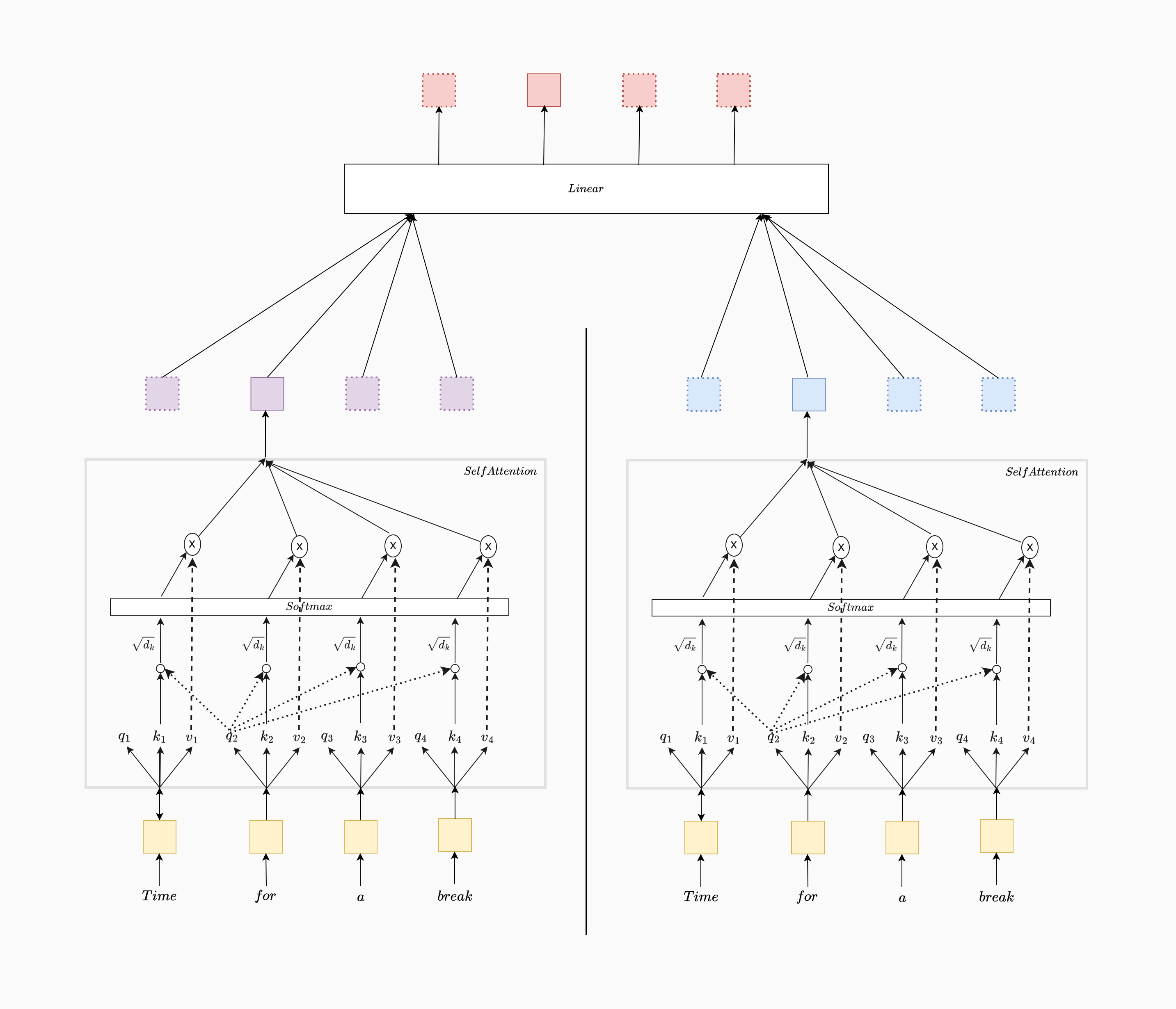
Implementation Approach

In our implementation for simplicity, we leverage the single-head self-attention mechanism as a building block. By creating multiple instances of the single-head attention module, each head computes attention independently on a different subspace of the embedding (with dimensionality embed_size / heads). Each head transforms the input using its own query, key, and value projections, then computes attention and produces an output vector for each token. These individual outputs from each head are then concatenated and passed through a final linear layer to merge the information back into the original embedding space.

Benefits of Multi-Head Attention

1. Parallel Attention Distributions: Each head learns to focus on different parts of the sequence independently, allowing the model to capture a range of dependencies and relationships.
2. Enhanced Representational Power: By learning attention weights across multiple subspaces, the model gains a richer understanding of the context, capturing both long-term and short-term dependencies.

class MultiHeadSelfAttention(nn.Module):
    def __init__(self, embed_size, heads):
        super(MultiHeadSelfAttention, self).__init__()

        self.heads = heads
        self.head_dim = embed_size // heads

        # Ensure embed_size is divisible by number of heads
        assert self.head_dim * heads == embed_size, "Embedding size needs to be divisible by heads"

        # Create multiple heads by instantiating SingleHeadSelfAttention
        self.attention_heads = nn.ModuleList(
            [SingleHeadSelfAttention(self.head_dim) for _ in range(heads)]
        )

        # Final linear layer to project concatenated output back to embed_size
        self.fc_out = nn.Linear(embed_size, embed_size)

    def forward(self, values, keys, query, mask=None):
        # Split input embedding into head_dim for each head
        seq_len = values.shape[1]

        values = values.view(seq_len, self.heads, self.head_dim)  # (sequence_length, heads, head_dim)
        keys = keys.view(seq_len, self.heads, self.head_dim)      # (sequence_length, heads, head_dim)
        queries = query.view(seq_len, self.heads, self.head_dim)  # (sequence_length, heads, head_dim)

        # Apply single-head attention for each head and store the results
        head_outputs = [
            attention_head(values[:, i, :], keys[:, i, :], queries[:, i, :], mask)
            for i, attention_head in enumerate(self.attention_heads)
        ]

        # Concatenate all heads along the embedding dimension
        out = torch.cat(head_outputs, dim=-1)  # (sequence_length, embed_size)

        # Project the concatenated output back to the original embedding size
        out = self.fc_out(out)  # (sequence_length, embed_size)

        return out